Abstract
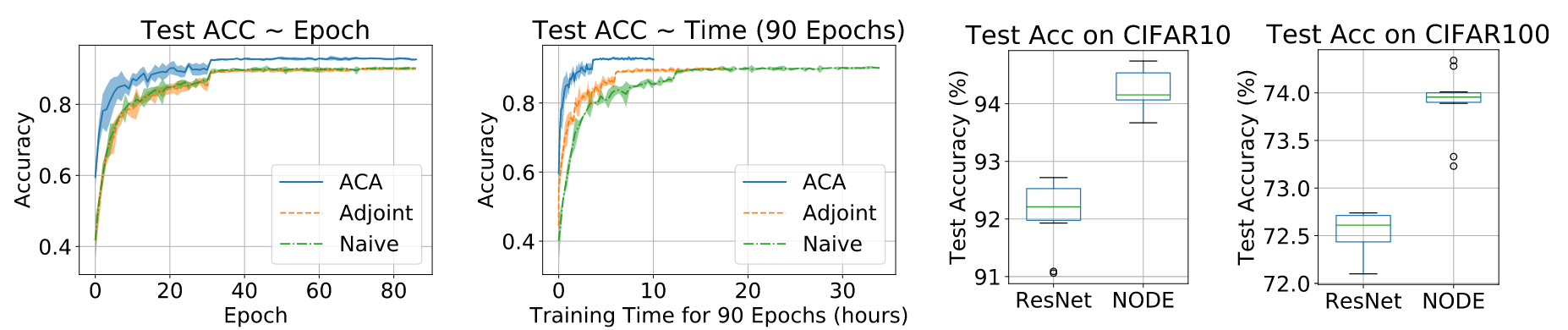
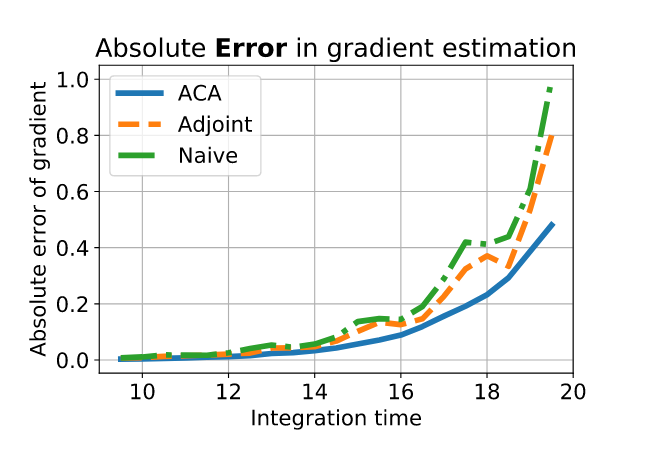
Neural ordinary differential equations (NODEs) have recently attracted increasing attention; however, their empirical performance on benchmarktasks (e.g. image classification) are significantlyinferior to discrete-layer models. We demonstratean explanation for their poorer performance is theinaccuracy of existing gradient estimation methods: the adjoint method has numerical errors in reverse-mode integration; the naive method directly back-propagates through ODE solvers, but suffers from a redundantly deep computation graph when searching for the optimal stepsize. We propose the Adaptive Checkpoint Adjoint(ACA) method: in automatic differentiation, ACA applies a trajectory checkpoint strategy which records the forward-mode trajectoryas the reverse-mode trajectory to guarantee accuracy; ACA deletes redundant components forshallow computation graphs; and ACA supports adaptive solvers. On image classification tasks, compared with the adjoint and naive method, ACA achieves half the error rate in half the training time; NODE trained with ACA outperforms ResNet in both accuracy and test-retest reliability. On time-series modeling, ACA outperforms competing methods. Finally, in an example of the three-body problem, we show NODE with ACA can incorporate physical knowledge to achieve better accuracy.
Problems with exisiting methods
Adjoint method suffers from numerical error

Naive method suffers from deep computation graphs
Adaptive Checkpoint Adjoint method
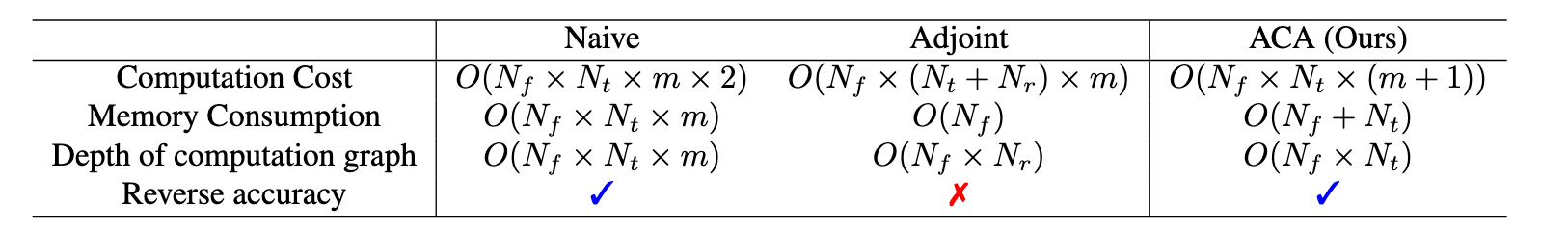
Experiments
Image Classification